Back then
When I was in college, I used to solve a lot of sequence problems. I really liked the topic. It is something that I cannot depict right now, because I have only a few words in my mind. Whatever I write here cannot express the importance of the sequences in mathematics. Nevertheless, I will try to explain the topic while giving my understanding. While learning sequences it is important to build a bridge between the mathematics we know right know, and the mathematics that we will know in the future.
I remember that the under-graduate mathematics have had began for me, when I started to learn the sequences and limits. It contains so much abstractness like epsilon-delta definitions. Or some proofs like you SHOULD memorize and implement into your brain like it is a little chip. Let us start with the definition of the sequence.
$\textbf{\small Definition 1.13.:} $ (Sequence) A sequence is a function whose domain is $\mathbb{N}$.
I know the definition is pretty straightforward and short. Consider the function $f$ defined as $f:\mathbb{N} \rightarrow \mathbb{R}$. And the domain $\mathbb{N}$ can be considered as the order of the list. For example the very first element of the function is $f(1)$ and, clearly the value of $f(1)$ is in $\mathbb{R}$ or in the corresponding range set. It is pretty true if you understood that the domain $\mathbb{N}$ stands for the index of the sequences. Let us give vivid examples,
Formatting the sequences
Consider the sequence $\left(1, \dfrac{1}{2}, \dfrac{1}{4}, \dfrac{1}{8}, \dots\right)$. One can infer that we can write it as $\left(\dfrac{1}{2^n}\right)^{\infty}_{n=0}$ or $(a_n)$, where $a_n=\dfrac{1}{2^n}, \ \forall n \in \mathbb{N}$. So using the definition we can find $f(1)$ which is $\dfrac{1}{2}$. See that $\dfrac{1}{2^n}: \mathbb{N} \rightarrow \mathbb{R}$ therefore it is valid to write either $f(1)$ or $a_1$. However, for the future cases we only use $a$, $b$ and so on to represent the sequences, rather than $f$ or $g$. It is a common naming convention. Our cumulative understanding says that there are sequences that converge nowhere or converges as it goes to infinity. Now we will give the definition for convergence.
$\textbf{\small Definition 1.14.:} $ (Convergence of a Sequence) Let $(a_n)$ be a sequence. If given any $\epsilon > 0$ there exist a number $N=N(\epsilon)$ such that $|a_n-L| < \epsilon$ whenever $n > N \in \mathbb{N}$, then $L$ is the limit of $(a_n)$ and denoted as $\lim_{n\rightarrow \infty} a_n = L$ or $a_n \rightarrow L$ as $n \rightarrow \infty$.
Where the f*ck epsilons or $N$’s come from? I would like to remind you that mathematicians are evil people who never let you know what mathematics really is. But we are Prometheus.
At first we consider a simple and non-complex sequence $a_n$. Let’s take a number $L$, which we will call the limit of the sequence, at the end of the operations. And also take veeeeery small and arbitrary positive real number $\epsilon$ (like $0.314 \times 10^{-999}$). Then look at some of the terms of the sequence $a_1$, $a_2$, $a_3$ and so on. Our aim is to find a number $N$ such that the absolute difference between the $n$th term of the sequence and the $L$ is smaller than $\epsilon$, whenever $n$ is bigger than the number $N$ we choose. Take a look at the image below.
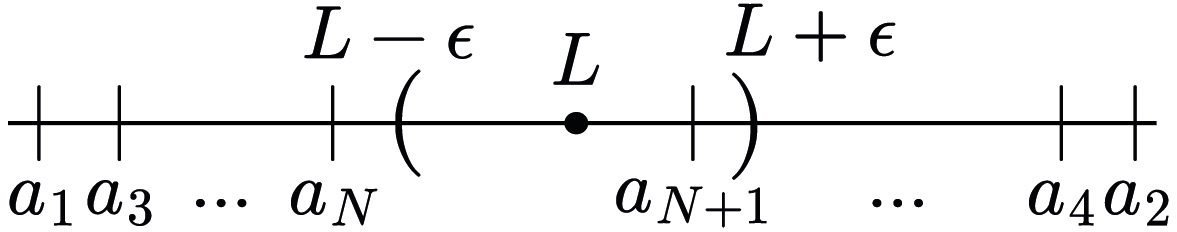
I have made up a sequence and wrote some terms of it. It bounces between left hand-side and right hand-side of the real line. But then there is an area among the parentheses with $L$ in the middle. That area is simply called $\epsilon$-neighbourhood of $L$ with edges $L-\epsilon$ and $L+\epsilon$. Remember the definition $|a_n-L| < \epsilon$ and $-\epsilon < a_n - L < \epsilon$ therefore $L-\epsilon < a_n <L+\epsilon$. We see that after $n$ passes some number $N$ we coincide into the $\epsilon$-neighbourhood of $L$. That is why, the definition is so intiutive yet so logical.
What if we do not have any end of the road situation? What if we have infinite sequence that does not converge to anywhere. Then we call it “divergence sequence”. Now that we understand the concept and also the definition we can move a bit further and give more abstract definition. It is exactly the same thing but with no words, just for fun 😀.
$\forall \epsilon > 0,\ \exists N=N(\epsilon) : |a_n - L |,\ \forall n > N \in \mathbb{N} \iff \lim_{n \rightarrow \infty} = L$
One example to rule them all
It took my days to understand the value and meaning of $\epsilon$ and $N$. But now I have solid understanding of the concept and I hope it helps to the people who struggles or struggled like me. Now, we go back to the high school and show the following statement $\lim_{n \rightarrow \infty}\dfrac{1}{n} = 0$.
$\textbf{\small Example:} $ Show that $\lim_{n\rightarrow \infty} \dfrac{1}{n} = 0$
Before writing the formal solution, let’s focus on the intuitive facts. To do that, let’s take $\epsilon = \frac{1}{500}$. The problem states that the sequence $\frac{1}{n}$, let’s call it $(a_n)$, eventually gets arbitrarily close to $0$. Since we have set $\epsilon = \frac{1}{500}$, this leads us to the following $\epsilon$-neighborhood: $ (L-\epsilon, L+\epsilon)=\left(0-\frac{1}{500}, 0+\frac{1}{500}\right)=\left(-\frac{1}{500}, \frac{1}{500}\right) $ centered around the limit $0$.
So, which terms of the sequence fall into this interval? The $500$th term, $a_{500} = \frac{1}{500}$, is on the boundary of this interval, not strictly inside it. However, for any $n>500$, the term $a_n$ will be in the interval $\left( -\frac{1}{500}, \frac{1}{500} \right)$. Remember that we want to find a number $N$ such that $|a_n-L| < \epsilon$ whenever $n > N$. In our case, $|\frac{1}{n}-0| < \frac{1}{500}$ simplifies to $\frac{1}{n} < \frac{1}{500}$, which is satisfied if $n > 500$. Thus, we can choose $N = 501$. (Of course, $N=500$ is also a correct choice, but we often choose $N=501$ to avoid any ambiguity at the boundary).
Let’s generalize this method for any arbitrary positive real number $\epsilon$. We write the inequality $|\frac{1}{n}-0|<\epsilon$, which is equivalent to $\frac{1}{\epsilon}<n$. Thus, choosing $N$ to be the integer part of $\frac{1}{\epsilon} + 1$ is sufficient. More rigorously, we can choose $ N = \left\lfloor \frac{1}{\epsilon} \right\rfloor+1 $. Now we can move on to the formal proof.
$\textbf{\small Proof:} $ Let $\epsilon > 0$ be given. Choose a natural number $N$ satisfying $N > \frac{1}{\epsilon}$. We have verified that the choice of $N$ has the desired property. Let $n \geq N (> \frac{1}{\epsilon})$. Then, the inequality $n > \frac{1}{\epsilon}$ implies $\epsilon > \frac{1}{n}$, and hence $|a_n - 0| < \epsilon$.
The logical procedure here is very similar to algorithm design in computer science. We can formalize these steps using the pseudo-code shown below.
FUNCTION findNaturalNumberN(epsilon)
Let epsilon > 0 be arbitrary
Show a choice for N
Show N works perfectly
Derive the inequality in definition using N
END FUNCTION
Let us use the procedure on the following example.
$\textbf{\small Example:} $ Show that $\left(\dfrac{n+1}{n}\right)_{n=1}^{\infty}=1$
We have to find a suitable value for $N$. Using the definition we write $|\frac{n+1}{n}-1|<\epsilon$. And we see that $|\frac{1}{n}|=\frac{1}{n}<\epsilon$. Same as above we choose an integer greater then $\frac{1}{\epsilon}$.
$\textbf{\small Proof:} $ Let $\epsilon > 0$ be given. Choose a number $N$ satisfying $N > \dfrac{1}{\epsilon}$. Let $n \in \mathbb{N}$ satisfy $n \geq N$. Then $n \geq N$ implies $n > \frac{1}{\epsilon}$, which is same thing as $\frac{1}{n} < \epsilon$.
One more example and then we will move to a new topic called uniqueness of limits.
$\textbf{\small Example:} $ Show that $\left(\dfrac{2n^3-3n+5}{3n^3-5n^2+5n-7}\right)_{n=1}^{\infty}=\dfrac{2}{3}$
Consider $\left|\dfrac{2n^3-3n+5}{3n^3-5n^2+5n-7} - \dfrac{2}{3}\right|$. We will try to find simpler yet bigger inequalities.
$\left|\dfrac{2n^3-3n+5}{3n^3-5n^2+5n-7} - \dfrac{2}{3}\right|$=$\left|\dfrac{8n^2-19n+29}{3(3n^3-4n^2+5n-7)}\right|$ $\leq$ $\left|\dfrac{8n^2-19n+29}{3n^3-5n^2+5n-7}\right|$
Observe that for $n\geq 0$ the inequality is positive therefore,
$\dfrac{8n^2-19n+29}{3n^3-5n^2+5n-7}$ < $\dfrac{8n^2+29}{3n^3-4n2}$ < $\dfrac{8n^2+8n^2}{3n^3-4n^2}$=$\dfrac{16}{3n-4}$<$\dfrac{16}{3n-4}$ = $\dfrac{16}{3}\cdot\dfrac{1}{n-2}$ < $\epsilon$
Lastly,
$n-2 > \dfrac{ 16}{3 \epsilon}$ and therefore, $n > \dfrac{16}{3\epsilon} + 2$. We can choose $N = \left\lfloor \dfrac{16}{3\epsilon}\right\rfloor+2$.
Uniqueness is what we want
It is not that surprising to learn the property that states “the limit of a sequence is unique”. Because no sequence can approaches to two different values for the same index.
$\textbf{\small Theorem 1.1.:} $ (The limit of a sequence is unique) If $\lim_{n\rightarrow \infty} a_n$ exists then it is unique.
$\textbf{\small Proof:} $ We will use proof by contradiction. Proof by contradiction is a powerful method of reasoning where you prove a statement is true by first assuming it’s false, and then showing that this assumption leads to a logical impossibility or an absurd result. Suppose that $\lim_{n\rightarrow \infty} a_n = L_1$ and $\lim_{n\rightarrow \infty} a_n = L_2$. Using the definition we have the followings:
$\lim_{n\rightarrow \infty} a_n = L_1,\ \forall \epsilon > 0,\ \exists N_1=N_1(\epsilon) : \forall n > N_1,\ |a_n-L_1| < \dfrac{\epsilon}{2}$
$\lim_{n\rightarrow \infty} a_n = L_2,\ \forall \epsilon > 0,\ \exists N_2=N_2(\epsilon) : \forall n > N_2,\ |a_n-L_2| < \dfrac{\epsilon}{2}$
Using triangle inequality from high-school knowledge,
$|L_1-L_2|$ = $|L_1-a_n + a_n - L_2|$ $\leq$ $|a_n - L_1| + |a_n - L_2|$ < $\dfrac{\epsilon}{2} + \dfrac{\epsilon}{2}$ = $\epsilon$. Observe that, for absolute value we have the following inequality $|L_1-L_2| \geq 0$. But we also have $\epsilon > |L_1-L_2|$. The only way out is $|L_1 - L_2| = 0$, which implies $L_1 = L_2$.
In the next section, we will talk about algebraic and order limit theorems. Thanks for reading.