The edges we all know
I guess everybody that has a little curious have met with Zeno. It is unclear but generally thought that Zeno paradoxes have been developed to support the Parmenides’ doctrins by Zeno of Elea. Do not worry we will not talk about neither Parmenides nor his absurd motion doctrins. By the way he said that “motion is nothing but an illusion”.
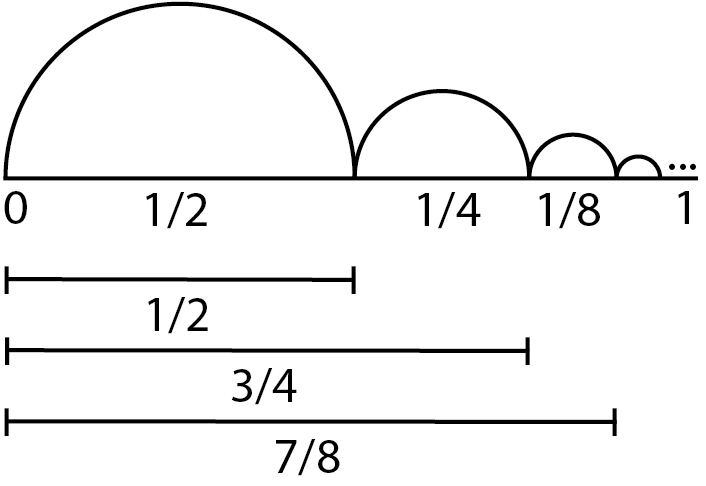
However, we will use Dichotomy paradox to address the topics infimum and supremum. Dichotomy paradox basically states that to travel any finite distance, you must complete infinite number of tasks using your finite amount of time, which is a paradox since there’s an infinite number of tasks corresponds to finite time, the journey can never be completed. Here is the process that Zeno followed: first decide a goal. Second go halfway of it and then go half of the remaining distance, and then repeat the process. Having to reach a halfway point goes on infinitely.
This paradox is fundementally related to the concepts of supremum and limit of a sequence. Think of a distance $D=1$. Zeno should cover the halfway of the distance at very first step. Let’s name it as $d_1=\frac{1}{2}$. For $d_2$ Zeno should go halfway of the $d_1$, which is $d_2=\frac{1}{4}$, similarly $d_3=\frac{1}{8}$. If we formulate it (Zeno did not know how to formualate it) we have $d_n=\frac{1}{2^{n}}$, where n is a step number.
Also, we conclude another formula by using direct intuition. The distance that we have traveled after $n$ steps is just partial sum of these distances, say $S_n$. For example, if we traveled for $n=5$ steps then $S_5=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}=31/32 \approx 0.96875$.
Supremum
So how is this paradox connected to supremum on a random set (ordered)? Well, the set of all possible positions $S$ is bounded above by $D=1$. So, we can write $\forall n \in \mathbb{N}, S_n < 1$. And as a result the supremum provides the final destination point as the smallest number that is greater than or equal to every point the traveler reaches. There is no such a point greater than 1 in $S_n$. If it’s not clear to you right now, don’t worry. When we discuss the limits of sequences, everything will become clearer and easier to understand, as we’ll explore concepts like boundedness, completeness, and monotonicity.
Infimum
As we can infer infimum is some kind of reverse of supremum. I am choosing my words carefully, a small mistake can lead us to misunderstanding the whole concept. The reverse refer to our intuition, not formal definition. Just to make the concept easier to understand. Similarly, the infimum $m$ of a set $S$ of real numbers is the greatest lower bound of the set. What we mean by saying greatest is there is no other lower bound that is smaller than $m$.
Some formality
As we give some intuition, it is safe to proceed to the formal definition. To begin with the definitions for bounded below and bounded above will be given and then we will build supremum and infimum.
$\textbf{\small Definition 1.9.:} $(Upper bound) Let $S$ be and ordered set (Definition 1.7) and $E \subset S$ if there is $M \in S$ such that $\forall x \in E$, $x \leq M$ we say that $E$ is bounded above and $M$ is upper bound of $E$
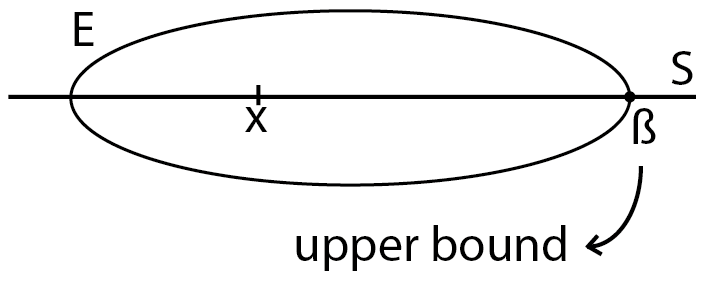
It seems easy to interpret the definition. We define such a number that bounds the set in some way (for real field it is a numerical bound). And we call that number upper bound of a set. We can think it as a border or edge of a set to make things easy to understand.
Similarly, we can define lower bound
$\textbf{\small Definition 1.10.:} $(Lower bound) Let $S$ be and ordered set and $E \subset S$ if there is $m \in S$ such that $\forall x \in E$, $x \geq m$ we say that $E$ is bounded below and $m$ is lower bound of $E$
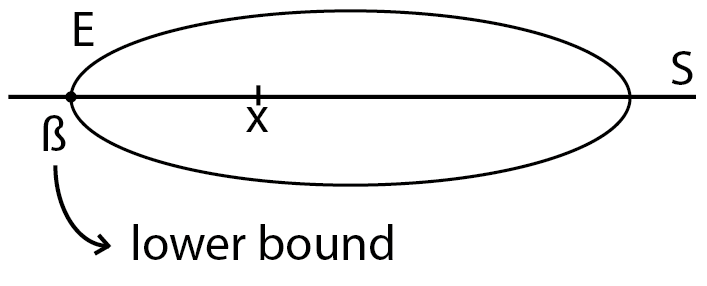
Since we have given the crucial definitions in Definition 1.9 and Definition 1.10, we can move on to more cruicials, which are called infimum and supremum. We need definition of upper bound to define supremum and not surprisingly definition of lower bound to define infimum.
$\textbf{\small Definition 1.11.:} $(Supremum) Let $S$ be an ordered set and $E \subset S$. If $M \in S$ is an upper bound of $E$ such that $M \leq M^{\prime}$ for every upper bound $M^{\prime}$ of $E$, then $M$ is called the supremum of $E$, denoted $M = \sup E$.
Definition is very straightforward. We have bunch of upper bounds on $E$, then we choose the one that is smaller than all of them. We choose the least upper bound.
$\textbf{\small Definition 1.12.:} $(Infimum) Let $S$ be an ordered set and $E \subset S$. If $m \in S$ is a lower bound of $E$ such that $m \geq m^{\prime}$ for every lower bound $m^{\prime}$ of $E$, then $m$ is called the infimum of $E$, denoted $m = \inf E$.
This is also easy to understand. We have some lower bounds on $E$, then we choose the biggest one. There we call it greatest lower bound.
Axiom of Completeness
Not surprisingly, until 1870s there were no construction of $\mathbb{R}$ from $\mathbb{Q}$ were present. Thanks to the mathematicians, Augustin Louis Cauchy, Bernhard Bolzano, Niels Henrik Abel, Peter Lejeune Dirichlet, Karl Weierstrass, and Bernhard Riemann we have now solid understanding of $\mathbb{R}$. By constructing the $\mathbb{R}$ they formalize the intuitive propert that was discovered to be missing from the rational numbers $\mathbb{Q}$. There was a problem called gap, and axiom of completeness solved it perfectly.
The problem we refer is basically a missing number problem. For example, take the set $S = \{r \in \mathbb{Q}\ | \ r^2 < 2\}$, which is bounded above but does not contain its $\sqrt{2}$ least upper bound because $\sqrt{2} \notin \mathbb{Q}$. So they saw that the rational numbers had “holes”, which we name them as irrational numbers. Intiutively, the axiom of completeness make certain that the real number line has no “gaps”. Let’s give the formal state.
$\textbf{\small Axiom of Completeness:} $ Every non-empty set of real numbers that is bounded above has a least upper bound (or supremum) that is a real number.
Consider the same example but with little difference. Take $S = \{r \in \mathbb{R}\ | \ r^2 < 2\}$, which is bounded above and contain the least upper bound $\sqrt{2}$. There are some theorems that build upon axiom of completeness such as: monotone convergence theorem, intermediate value theorem, Cauchy criterion for convergence and so on. We will prove them a bit later.
In the next section, we will talk about sequences and their limits. Thanks for reading.