Build the intervals and stay inside

Whenever I talk about mathematics, I directly think of number sets. It is surprisingly hard to build, yet easy to understand. Each of them have a different purpose, there is a very close relation between them. Until we prove the properties and maybe the existence of the number sets we will use $\mathbb{R}, \ \mathbb{N}, \ \mathbb{Z}, \ \mathbb{Q}, \ \mathbb{C}$ without proving the properties, as if we all accept and embrace them. Further, Even I won’t talk about Peano’s axioms.

Let us formally define the intervals

$ \textbf{Definition 1.4.:} $ An interval is a set of real numbers between two other numbers.

Short, yet strong definition. Don’t confuse yourself on the term “real”, it could be natural numbers, rational numbers, or integers. Intervals can be defined in different forms. Let us write down every possibility we have

$$ (a,b) = \{x \in \mathbb{R} : a < x < b\} \newline [a,b] = \{x \in \mathbb{R} : a \leq x \leq b\} \newline [a,b) = \{x \in \mathbb{R} : a \leq x < b\} \newline (a,b] = \{x \in \mathbb{R} : a < x \leq b\} \newline (a, \infty) = \{x \in \mathbb{R} : a < x \} \newline (- \infty, b] = \{x \in \mathbb{R} : x \leq b\} \newline [a, \infty) = \{x \in \mathbb{R} : a \leq x \} \newline (- \infty, b) = \{x \in \mathbb{R} : x < b\} \newline (a, \infty) = \{x \in \mathbb{R} : a < x \} \newline (-\infty, \infty) = \mathbb{R} $$

There are some naming conventions mathematicians often use. For instance $(a,b), \ (a, \infty), \ (- \infty, b), \ (a, \infty)$ and $(-\infty, \infty)$ are called open intervals. Logically, $[a,b]$ is called closed interval and the rest of them that includes both $[$ and $($ are called semi-open or semi-closed interval.

To hug thyself

What a title huh? I named it like that because it perfectly reflects the subsets. Being a subset is like tearing thyself apart. After tearing apart you can name those pieces “subsets”. With braveity you can scream “those are my subsets!”. Mathematicians, of course as always, use a symbol to show a subset relation between sets. If $x$ is a subset of $y$ then we write $x \subseteq y$. Further than that if $x \neq y$, then it is very convenient to use $x \subset y$.

Some well-known subset relation is following: $\mathbb{N} \subseteq \mathbb{Z} \subseteq \mathbb{Q} \subseteq \mathbb{R}$. Therefore, we can freely say that every natural number is integer, every integer is rational number and every rational number is a real number.

One set can be subset of itself. As title says $x$ can hug thyself. Namely, $x \subseteq x$. It is analogic to writing $1=1$. We will use some proof techniques in further topics. Sometimes we are asked to prove that sets are equal, that is when we use the if and only if part of mathematics. I know, it sounds silly right now. However, if you prove that a set $x$ is a subset of $y$ and $y$ is a subset of $x$ then you directly proved that the sets are equal to each other, namely $x=y$.

I used to use two-segment proofs for those cases. Generally, I used to prove the $\Rightarrow$ first and then I used to prove $\Leftarrow$. We’ll see a lot of examples for that, do not worry.

Gnothi seauton (Know thyself)

Another strange naming I used. Dealing with sets is often annoying, thanks to its simplicity, yet complexity. In some cases, a set includes another sets as an element. For example, let $A = \{a,b, \{c,d\}\}$. As you might anticipate we cannot write $c \in A$, yet we can write $\{c,d\} \in A$. Further if we let $B=\{c,d\}$ then $B \subset A$.

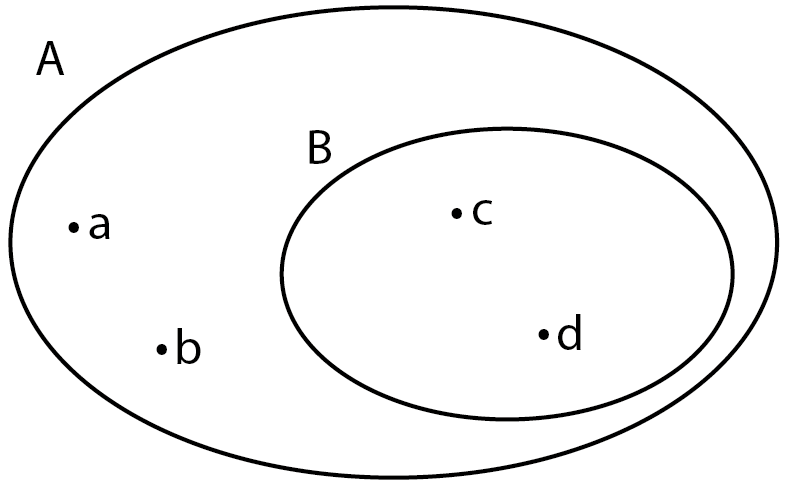
Also a classical statement implies that the empty set is a subset of all sets, more rigorously $\forall A \subset E, \ \empty \subset A$. It looks like as if I used another language to represent what I said at the beginning of the paragraph. I want to tell more about the esotericism of mathematics. Mathematicians made up symbols to hide their witchcraft from ordinary people.

I do not prefer to tell them all at once and then never mention, rather I prefer to use it more. For example, the symbol $\forall$ stands for “for all” phrase, $E$ stands for universal set (the set that includes every set imaginable), $A$ stands for arbitrary set from $E$. Therefore, this esoteric phrase can be translated to the following sentence “for all subset A of E, empty set is a subset of A” or in simpler words “the empty set is a subset of all sets”.

Without giving any formal proof, we can prove that statement. So we want to prove that for an arbitrary set $A$, an empty set is subset of $A$. Further, every element in empty set is also an element of $A$. Now, let us consider contradictive side of the statement. Say that $A$ be an arbitrary set and $\empty \not\subset A$. Then by definition of subset, we can say that there $\exist x \in \empty$ that is $x \notin A$, which contradicts the definition of $empty$ set because $\empty$ set has no elements in it. Therefore, our statement is true and $\forall A \subset E, \ \empty \subset A$ holds.

I used another symbol to imply “there exist” phrase, namely $\exist$. During my under-grad study I used and saw these symbols a lot. After a while those are the new language I learnt. Two years ago, my mother language consisted of those symbols. I was thinking and writing that way. So the key to understanding the symbols is to use it in a daily basis.

Sets of subsets or hat-trick

There is a set that contains the subsets of the main set. It is called power set. By saying main I mean the set that we are trying to find its subsets. For example, by applying the following method, we can write down every subset that can be formed from the set $A=\{a,b,c\}$.

Take first the singletons. Let us use the letter $\mathcal{P}$ to address the the power set. And use the symbol convention $\mathcal{P}(\mathbb{A})$ to clearly show the power set of the set $A$. First, we construct the singleton sets; $\empty, \ \{a\}, \ \{b\}, \ \{c\}$. Then construct the pairs; $\{a,b\}, \ \{b,c\}, \ \{a,c\}$. Finally the set itself; $\{a,b,c\}$. We have exactly $8$ subsets, and it is certain that there cannot be any more. So we can write

$ \mathcal{P}(\mathbb{A})=\{ \empty,\{a\},\{b\},\{c\}, … ,\{a,b,c\} \} $ where $A=\{a,b,c\}$

I named this section as hat-trick because we never know what will come out of the hat or set. If the magician is skilled, we can’t predict how many rabbits will come out of the hat. In fact, we can’t even predict if a rabbit will come out of the hat at all. We think of a rabbit, a pigeon appears, and we are once again the surprised ones.

Ordering and conquering the sets

Before we continue with ordering the sets. We will give the conditions required for a set to be a subset. Let us define first the relation.

$\textbf{Definition 1.5.:} $ (Order) A $\textit{relation}$ is any subset of a Cartesin product.

For example, a subset of $A \times B$, called a relation from $A$ to $B$.

$\textbf{Definition 1.6.:}$ (Partial Order) A relation $\leq$ is a partial order on a set $A$ if it satisfies following conditions

1-) Reflexivity: $a \leq a, \ \forall a \in A$
2-) Antisymmetry: $a \leq b $ and $\ b \leq a \ \Rightarrow \ a=b$
3-) Transitivity: $a \leq b $ and $\ b \leq c \ \Rightarrow \ a \leq c$

A real world example is as follows: let $A \subseteq B$ and $B \subseteq C$ are sets. Then the followings are satisfied,

1-) Reflexivity: $A \leq A, \ \forall A \in E$
2-) Antisymmetry: $A \leq B $ and $\ B \leq A \ \Rightarrow \ A = B$
3-) Transitivity: $A \leq B $ and $\ B \leq C \ \Rightarrow \ A \leq C$

Finally we can give the definition of partially ordered set.

$\textbf{Definition 1.7.:}$ (Partially Ordered Set) A partially ordered set (poset) is a set P with a binary relation $\leq$ on $P$.

For example, The set of real numbers $\mathbb{R}$, equipped with the standard “less than or equal to” relation $\leq$, is a partially ordered set. It is very important to understand this concept completely, because we will use this definition to form some of the main components of the Analysis.

Counting one by one

Counting on a set is not as easy as you might think. It is something hard to understand and build. We can talk about finite set and infinite set without proving anything. Just by using our assumptions. I have said before that set theory is simple yet complex. Both at the same time. And counting is one of the same time topic. Since our main aim is to understand and talk about the analysis, we will not give any further proof here.

To show and indicate the number of elemens in a set we use $|$ symbol as follows $|A|$ where $A$ is a set, also another notation $s(A)$ can be used. If a set is infinite than we simply write $|A| = s(A)=\infty$. Let us give some properties on finite sets.

$\textbf{Lemma 1.1.:}$ $A \subset B$, then $|A| \leq |B|$

and

$\textbf{Lemma 1.2.:}$ $A \leq B$ and $|A| = |B|$, then $A = B$

are trivial. Enthusiasts can look at the topic of “ordinal numbers and cardinal numbers” to better understand counting the elements of a set.

Archimedean property

Think of any number, for example, $124814412881421.124124$. Can you find bigger number than this? Well, by using your personal experiences and gut feeling you will say yes to the question. So, somebody from Provincia di Siracusa had also thought of it. Therefore, we call this property by its name Archimedean. Let us give the definition and then try to understand word by word.

$\text{Definition 1.8.:}$ (Archimedean Property) An ordered field $F$ has the Archimedean Property if, given any positive $x$ and $y$ in $F$ there is an integer $n > 0$ so that $nx > y$.

So a straightforward question comes to mind “what is a field?”. For now, it is enough if we know field is a set that has two operations. A field is basically a “number system” where you can add, subtract, multiply, and divide (except by zero) and all the usual algebraic rules hold. To illustrate, So $\mathbb{R}$ is a field, and we often describe it as a complete ordered field.

Did you see? An ordered field F directly address the $\mathbb{R}$. Therefore, Archimedean property will hold on $\mathbb{R}$.

Whenever we choose two numbers on $\mathbb{R}$, like $1.32451, \ 3.24233 \in \mathbb{R}$. Then we can find an integer $n$ such that $n \cdot 1.32451 > 3.24233$. By simple calculation we find $n=3$, because $3 \cdot 1.32451 = 3,97353 > 3,24233$.

In the next section, we will talk about infimum, supremum, fields and the real field. Thanks for reading.