In this blog we use so called LaTeX to represent the mathematical terms. To sustain and maintain the beauty of the mathematics it is SO necessary to use LaTeX. Let’s start with the very well-known definition in mathematics. We will start with definition of a set, some basic properties of sets, representation choices of sets, operations on sets.
Neat start to set theory
$ \textbf{Definition 1.1.} : \text{A set is a collection of objects called elements.} $
For example, countries in the world, schools in a city, students in a school can be called as set. There if we say $A$ is a country in the world $W$ then we can write $A \in W$. Let’s give a few properties and symbols of sets.
$ \textbf{Definition 1.2.} \newline 1. \ x \ \text{is an element of} \ S \ \text{if and only if} \ x \in S \newline 2. \ x \ \text{is not an element of} \ S \ \text{if and only if} \ x \notin S \newline 3. \ \text{Each element in} \ A \ \text{is also an element of} \ B \ \text{if and only if} \ A \subseteq B. \newline 4. \ A \ \text{and} \ B \ \text{are equal if and only if} \ A = B \ \text{provided that} \ A\subseteq B \ \text{and} \ B\subseteq A. \newline 5. \ \text{If} \ A \subseteq B \ \text{and} \ A \neq B \ \text{then} \ A \ \text{is a proper subset of} \ B. \ \text{We write} \ A \subset B. \newline 6. \ \text{Empty set is written as} \ \emptyset. \newline $
On our previous example, we say that countries in the world, schools in a city, students in a school can be called as set. But we made a crucial mistake. Because an element of mathematical set should also be mathematical. Therefore, when we say set, we can directly think integers, functions, natural number, real numbers, rational numbers and also sets. Sets can be written in different ways, there is no such a thing called one set representation. It is not unique.
For example we can either write $$A = \{1,2,3,4\}$$ or $$A = \{x : x \ \text{is a positive integer less than and equal to} \ 4\}$$ or $$A = \{1,…,4\}$$
To draw a set
In the last representation we understand that it begins with $1$ and continue until $4$, and also we anticipate that there is a no silly number inbetween. Thanks to human intuition. We have some so called sets such as natural numbers $\mathbb{N}$, integers $\mathbb{Z}$, rational numbers $\mathbb{Q}$, real numbers $\mathbb{R}$, and complex numbers $\mathbb{C}$. We encounter those sets so frequently. Mathematicians often state problems using these sets. For example, we can see such problems that starts with the following holy sentence “$\text{let} \ x \in \mathbb{R}$”.
And also a very important fact about the set is uniqueness of the elements. What I mean is there cannot be two identical elements in the same set. For example, when we write $\{a, a, b\}$ we mean $\{a,b\}$. This works when we are dealing with the equality of sets ($\text{Definition 1.2.4}$). For instance the set $B$ which has the solutions to the following equation $(x-1)(x-2) = 0$ is equal to the set $A={1,2}$.
We draw sets to anticipate the concept deeply, which we call Wenn diagram. Let the set be $x=\{y,z,t, \{a,b,c\}\}$
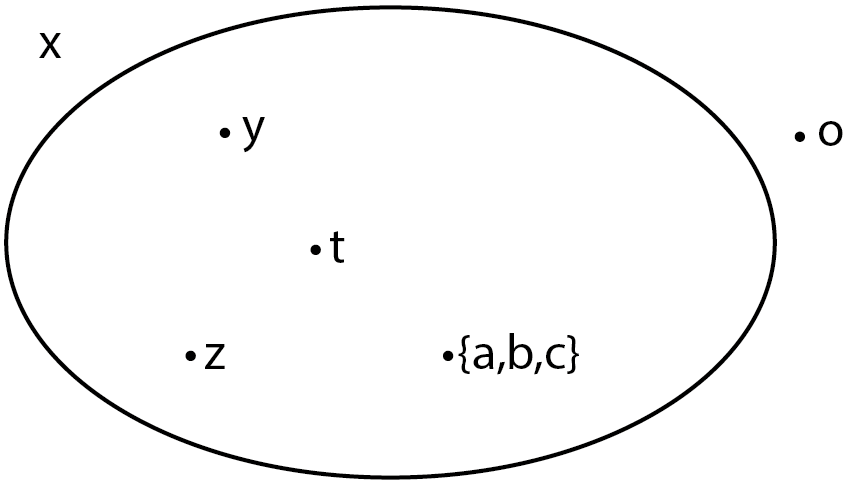
Let’s tear this diagram into pieces. We see that $y \in x$, $z \in x$, $t \in x$. Not surprisingly, we write $\{a,b,c\} \in x$. But, $a,b,c,o \notin x$. Fun fact: we can create a set with empty set and at the end we have not empty set. Let’s say $e$ is empty set and defined as $e = \{\emptyset, \{\{\emptyset\}\} \}$. So, the elements of $e$ are $\emptyset$ and $\{\{\emptyset\}\}$, but $\{\emptyset\}$ is not an element of $e$.
Importance of sets
In short, we can write sets as $A = \{x \in \mathrm{X} : P(x)\}$. This means that the set $A$ has such elements that satisfy the condition $P(x)$.
It is very important to understand it deeply because in the very far future we will examine open balls, which is a very crucial topic of topology. Open ball or Euclidean ball is defined as $B_r(p) = \{x \in \mathrm{M} | d(x,p) < r\}$, where $M$ is a set with metric d, and let $r \in \mathbb{R}$. It is not our topic yet, but even the example shows that everything in mathematics is defined using sets.
Other operations
There are four more operations, that I want to mention. Namely, union, intersection, complement, difference and cartesian product.
$ \textbf{Definition 1.3.} \newline 1. A \cup B = \{x : x \in A \ \text{or} \ x \in B\} \ \text{A union B} \newline 2. A \cap B = \{x : x \in A \ \text{and} \ x \in B\} \ \text{A intersection B} \newline 3. A^{c} = A^{\prime} = \{x : x \in U \ \text{and} \ x \notin A\} = U-A = U $\$ A \ \text{complement of A} \newline 4. A \setminus B = \{x : x \in A \ \text{and} \ x \notin B\} \ \text{A difference B} \newline 5. A \times B = \{(a,b) : a \in A \ \text{and} \ b \in B\} \ \text{A cartesian product B} \newline $
The following part will include intervals, subsets, number of elements in the sets, some examples of union, intersection and difference and lastly but most importantly Archimedean property.